The difficulty with creating a fully-automated solution is that it would require you to hardcode into your solution certain assumptions about the input images you are going to process. If these assumptions don't hold for all the potential images you may come across, the fully-automated solution won't give trustworthy results, and trying to extend the fully-automated solution to handle all possible inputs will likely cause it to bloat into an incomprehensible and complicated mess of code.
When in doubt about the variability in features of your input images, a solution like Jacob's with some user interaction is generally best. If you can be certain that the features of your input images follow a strict set of rules, then an automated solution can be considered.
As an example, below is some automated code I wrote to approximate the area under the red curve in your graph. Since I used the above graph as a guide, there are a number of conditions that must be met for it to work:
- The red pixels of the plotted line must be uniquely described in the image as containing green and blue color components equal to 0 and red color components equal to 1.
- The green pixels of the grid lines must be uniquely described in the image as containing red and blue color components less than 1 and green color components equal to 1.
- The blue pixels of the axes lines must be uniquely described in the image as containing red and green color components equal to 0 and blue color components equal to 1.
- The grid and axis lines must always be exactly aligned in a horizontal or vertical direction.
- The length of the grid lines must span well over half the width and height of the image.
- The x axis must be the longest horizontal blue line in the image.
- The grid lines must always be 1 pixel thick.
Subject to the above conditions on the input image, the following code can be used to approximate the area under the red curve without user input:
[img,map] = imread('original_chart.gif'); %# Read the indexed image
[r,c] = size(img); %# Get the image size
redIndex = find((map(:,1) == 1) & ... %# Find the red index value
(map(:,2) == 0) & ...
(map(:,3) == 0))-1;
greenIndex = find((map(:,1) < 1) & ... %# Find the green index value
(map(:,2) == 1) & ...
(map(:,3) < 1))-1;
blueIndex = find((map(:,1) == 0) & ... %# Find the blue index value
(map(:,2) == 0) & ...
(map(:,3) == 1))-1;
redLine = (img == redIndex); %# A binary image to locate the red line
greenLine = (img == greenIndex); %# A binary image to locate the grid lines
blueLine = (img == blueIndex); %# A binary image to locate the axes lines
w = mean(diff(find(sum(greenLine,1) > r/2))); %# Compute unit square width
h = mean(diff(find(sum(greenLine,2) > c/2))); %# Compute unit square height
squareArea = w*h; %# Compute unit square area
[maxValue,maxIndex] = max(redLine); %# Find top edge of red line
x = find(maxValue > 0); %# Find x coordinates of red line
y = maxIndex(maxValue > 0); %# Find y coordinates of red line
[maxValue,maxIndex] = max(sum(blueLine,2)); %# Find row index of x axis
y = maxIndex-y; %# Zero the y coordinate
totalArea = trapz(x,y)/squareArea; %# Compute the area under the curve
Which gives the following results:
squareArea = 460.6 square pixels
totalArea = 169.35 m*h
EXPLANATION:
I'll elaborate more about the steps involved in computing w:
- The binary image
greenLine is summed along each column using the function SUM, giving a 1-by-c vector where each element is a count of how many grid line pixels are in each column of the image.
- The elements of this vector that are greater than
r/2 (half the number of rows in the image) indicate columns of the image that contain a vertical grid line. The indices of these columns are found using the function FIND.
- The pairwise differences between these column indices are found using the function DIFF. This gives a vector containing the widths (in pixels) of the spaces between grid lines.
- Finally, the function MEAN is used to compute the mean width of the spaces between all the grid lines in the image.
When computing h, the only difference is that the sum is performed along each row and r/2 is replaced with c/2 (half the number of columns in the image).

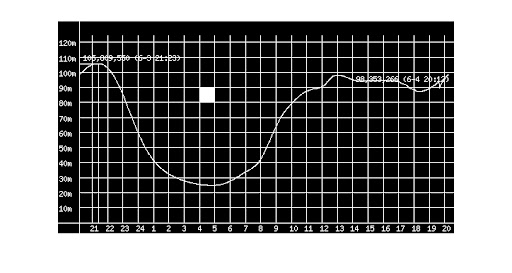 Figure 2
Figure 2