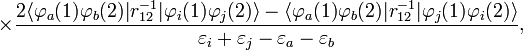Suggestions on syntax to express mathematical formula concisely

Question

Hello.

I am developing functional domain specific embedded language within C++ to translate formulas into working code as concisely and accurately as possible.

I posted a prototype in the comments, it is about two hundred lines long.

Right now my language looks something like this (well, actually is going to look like):

// implies two nested loops j=0:N, i=0,j
(range(i) < j < N)[T(i,j) = (T(i,j) - T(j,i))/e(i+j)];

// implies summation over above expression
sum(range(i) < j < N))[(T(i,j) - T(j,i))/e(i+j)];

I am looking for possible syntax improvements/extensions or just different ideas about expressing mathematical formulas as clearly and precisely as possible (in any language, not just C++).

Can you give me some syntax examples relating to my question which can be accomplished in your language of choice which consider useful. In particular, if you have some ideas about how to translate the above code segments, I would be happy to hear them.

Thank you.

Just to clarify and give an actual formula, my short-term goal is to express the following

expression concisely where values in <> are already computed as 4-dimensional arrays.

Answer 1

T = T - T'/e;

or, if you're not operating on all of T

T(0:i,0:j) = T(0:i,0:j) - T(0:i,0:j)'/e(0:i,0:j)

Answer 2

I would prefer a more solid separation between loops. For example, I'd prefer this alternative notation to your second example:

sum(range(j) < N)[sum(range(i) < j)[(T(i,j) - T(j,i))/e(i+j)]]

I also find the range syntax difficult. I think a range should be a single component. I'd prefer something like so:

j = range_iter(0,N)

That would open for range x(0,N); j = range.begin(); or alternatives I can't think up right now.

You could even:

j = range_iter(inc(0) => exc(N)); for j iterates over [0,N).

Anyway, interesting idea. Can your resulting functions be composed? Can you request domain information?

Answer 3

I'm not familiar with Phoenix and can only make assumptions about it's capabilities.

I've always liked the way Haskell allows me to express ranges as a list comprehension. It translates nicely from the actual mathematical notation into the programming language construct.

[ i + j | i <- [1..10], j <- [1..10] ]

would end up as something like:

[ i + j | i = range(1,10), j = range(1,10) ]

Unfortunately I really don't know if something like this is even possible with Phoenix.

Answer 4

If you're going to be writing this for the ab-initio world (which I'm guessing from your MP2 equation) you want to make it very easy and clear to express things as close to the mathematical definition that you can.

For one, I wouldn't have the complicated range function. Have it define a loop, but if you want nested loops, specify them both:

So instead of

(range(i) < j < N)[T(i,j) = (T(i,j) - T(j,i))/e(i+j)];

use

loop(j,0,N)[loop(i,0,j)[T(i,j) = (T(i,j) - T(j,i))/e(i+j)]]

And for things like sum and product, make the syntax "inherit" from the fact that it's a loop.

So instead of

sum(range(i) < j < N))[(T(i,j) - T(j,i))/e(i+j)];

use

sum(j,0,n)[loop(i,0,j)[(T(i,j) - T(j,i))/e(i+j)]]

or if you need a double sum

sum(j,0,n)[sum(i,0,j)[(T(i,j) - T(j,i))/e(i+j)]]

Since it looks like you're trying to represent quantum mechanical operators, then try to make your language constructs match the operator on a 1-1 basis as closely as possible. That way it's easy to translate (and clear about what's being translated).

EDITED TO ADD

since you're doing quantum chemistry, then it's fairly easy (at least as syntax goes). You define operators that always work on what's to the right of them and then the only other thing you need are parenthesis to group where an operator stops.

Einstein notation is fun where you don't specify the indices or bounds and they're implied because of convention, however that doesn't make clear code and it's harder to think about.

For sums, even if the bounds implied, they're always easy to figure out based on the context, so you should always make people specify them.

sum(i,0,n)sum(j,0,i)sum(a,-j,j)sum(b,-i,i)....

Since each operator works to the right, its variables are known, so j can know about i, a can know about i and j and b can know about i,j, and a.

From my experience with quantum chemists (I am one too!) they don't like complicated syntax that differs much from what they write. They are happy to separate double and triple sums and integrals into a collection of singles because those are just shorthand anyway.

Symmetry isn't going to be that hard either. It's just a collection of swaps and adds or multiplies. I'd do something where you specify the operation which contains a list of the elements that are the same and can be swapped:

c2v(sigma_x,a,b)a+b

This says that a and b are can be considered identical particles under a c2v operation. That means that any equation with a and b (such as the a+b after it) should be transformed into a linear combination of the c2v transformations. the sigma_x is the operation in c2v that you want applied to your function, (a+b). If I remember correctly, that's 1/sqrt(2)((a+b)+(b+a)). But I don't have my symmetry book here, so that could be wrong.

Answer 5

I don't like the way you specify that "triangular" 2d range. I'd like to see something like:

(i,j) in range(0..j,0..N)

for example, which could then lead to:

X = sum(f(i,j) for (i,j) in range(0..j,0..N));

AFAIK This is not an existing language, but since you're creating your own syntax... I'm doubtful about the ability to use j in the range expression for i, but you found a way in yours :-)

Answer 6

I would consider expressing math formulas as they are done in LaTeX. After all, LaTeX is already well-defined and well-documented in this area.

Answer 7

I am not sure how complicated those formulas will be, but if get to the point when your API looks more like that math domain than standard C++ (which is using operator overloading and template metaprogramming done quite easily), I would guess you should consider developing a Domain Specific Language (DSL). When you are trying to do it in a language (like in your case) it is called internal DSL and although it has some advantages, it has many disadvantages. You should know your requirements best, however I want to suggest you looking at tools for external DSLs, which are small external languages specialized for certain domain. Look at Jetbrains MPS and Eclipse Xtext, those are two open source tools, which can be used for rapid external DSL development.

Answer 8

my prototype (still needs lots of work obviously, and comments)

// #include "tensor/tensor.hpp"
// #include "typename.hpp"

#include <boost/spirit/home/phoenix/core/argument.hpp>
#include <boost/spirit/include/phoenix_core.hpp>
#include <boost/spirit/include/phoenix_operator.hpp>

#define BOOST_FUSION_INVOKE_FUNCTION_OBJECT_MAX_ARITY PHOENIX_ARG_LIMIT
#include <boost/fusion/functional/invocation/limits.hpp>
#include <boost/fusion/functional.hpp>

#include <boost/fusion/include/intrinsic.hpp>
#include <boost/fusion/include/vector.hpp>
#include <boost/fusion/include/algorithm.hpp>
#include <boost/fusion/include/vector_tie.hpp>
#include <boost/fusion/include/make_vector.hpp>

#include <boost/typeof/typeof.hpp>

namespace range_ {
    namespace detail {

        namespace phoenix = boost::phoenix;
        namespace fusion = boost::fusion;

        /// undefined or implicit object
        struct undefined {};

        template<int N>
        struct index {
            // index(boost::phoenix::argument<N>) {}
            typedef phoenix::actor<phoenix::argument<N> > argument;
            argument arg() const { return argument(); }
        };

        template<typename T, typename U = void>
        struct functional {
            typedef phoenix::actor<phoenix::value<T> > type;
            static type form(const T& t) { return type(t); }
        };

        template<typename T, typename U>
        struct functional<phoenix::actor<T>, U> {
            typedef phoenix::actor<T> type;
            static type form(const T& t) { return type(t); }
        };

        template<typename T>
        struct functional<undefined,T> {
            typedef typename functional<T>::type type;
            static type form(const undefined&) { return type(T()); }
        };

        template<int N, class L, class U, class T = undefined>
        struct expression;

        template<int N, class L, class U, class C>
        struct expression {
            typedef functional<L,U> lower_function;
            typedef functional<U,L> upper_function;

            expression(const L &lower, const U& upper, const C &cdr)
                : lower_(lower), upper_(upper), cdr_(cdr) {}

            template<class E>
            expression<N, L, U, E> operator()(const E &c) const {
                return expression<N, L, U, E>(lower_,  upper_, c);
            }

            template<class F>
            void operator[](const F &f) const {
#define TEXT(z, n, text) text
#define UNDEFINED_ARGUMENTS BOOST_PP_ENUM(PHOENIX_ARG_LIMIT, TEXT, undefined())
                evaluate<int>(f, fusion::make_vector(UNDEFINED_ARGUMENTS));
#undef TEXT
#undef UNDEFINED_ARGUMENTS
            }

            L lower_;
            U upper_;
            C cdr_;

            const L& left() const { return lower_; }

            const C& cdr() const {return cdr_; }

            template<typename T>
            typename functional<L,T>::type begin() const {
                return functional<L,T>::form(lower_);
            }

            template<typename T>
            typename functional<U,T>::type end() const {
                return functional<U,T>::form(upper_);
            }

            template<typename T, class F, class A>
            void evaluate(const F &f, const A &arguments) const {
                T i = this->begin<T>()(arguments);
#define AS_VECTOR(var, expr) BOOST_AUTO(var, fusion::as_vector(expr))
#define ADVANCE_C(seq) fusion::advance_c<N>(fusion::begin(seq))
                AS_VECTOR(b, fusion::erase(arguments, ADVANCE_C(arguments)));
                AS_VECTOR(a, fusion::insert_range(b, ADVANCE_C(b),
                                                  fusion::vector_tie(i)));
#undef ADVANCE_C
#undef AS_VECTOR
                while (fusion::invoke_function_object(this->end<T>(), a)) {
                    this->apply<T>(cdr_, f, a);
                    ++i;
                }
            }

            template<typename T, class E, class F, class V>
            void apply(const E &e, const F &f, const V &variables) const {
                e.template evaluate<T>(f, variables);
            }

            template<typename T, class F, class V>
            void apply(const undefined&, const F &f, const V &variables) const {
                fusion::invoke_function_object(f, fusion::as_vector(variables));
            }

        };

        template<int N, class  L, class U>
        expression<N, L, U>
        make_expression(const L &lower, const U& upper) {
            return expression<N, L, U>(lower, upper, undefined());
        }

        template<int N, class  L, class U>
        expression<N, L, U>
        make_expression(const expression<N, L, undefined> &expr, const U& right) {
            return expression<N, L, U>(expr.left(), right, undefined());
        }

        template<int N1, class L1, class U1, class T1,
                 int N2, class L2, class U2>
        expression<N2, L2, U2, expression<N1, L1, U1, T1> >
        operator,(const expression<N1, L1, U1, T1> &e1,
                  const expression<N2, L2, U2> &e2)  {
            return e2(e1);
        }

#define ARGUMENT(N) phoenix::actor<phoenix::argument<N> >
#define ACTOR_COMPOSITE(O,L,R)                                          \
        phoenix::actor<typename phoenix::as_composite<O, L, R>::type>


#define LOWER_BOUND_OPERATOR(op, eval, param)                           \
        template <typename T, int N>                                    \
        expression<N, param, undefined>                                 \
        operator op (const param& left, const index<N> &i) {            \
            return make_expression<N>(left, undefined());               \
        }


#define UPPER_BOUND_OPERATOR_INDEX(op, eval, param)             \
        template <typename T, int N>                            \
        expression<N, undefined,                                \
                   ACTOR_COMPOSITE(eval, ARGUMENT(N), param)>   \
        operator op (const index<N> &i, const param& e) {       \
            return make_expression<N>(undefined(),              \
                                      (ARGUMENT(N)() op e));    \
        }

#define UPPER_BOUND_OPERATOR_EXPRESSION(op, eval)                       \
        template <typename T, int N, class E>                           \
        expression<N, E, ACTOR_COMPOSITE(eval, ARGUMENT(N), T)>         \
        operator op (const expression<N, E, undefined> &left,           \
                     const T& right) {                                  \
            return make_expression(left, (ARGUMENT(N)() op right));     \
        }

#define UPPER_BOUND_OPERATOR(op, eval)                                  \
        UPPER_BOUND_OPERATOR_INDEX(op, eval, T)                         \
        UPPER_BOUND_OPERATOR_INDEX(op, eval, phoenix::actor<T>)         \
        UPPER_BOUND_OPERATOR_EXPRESSION(op, eval)

        LOWER_BOUND_OPERATOR( < , phoenix::less_eval, T)
        LOWER_BOUND_OPERATOR( < , phoenix::less_eval, phoenix::actor<T>)
        LOWER_BOUND_OPERATOR( <= , phoenix::less_equal_eval, T)
        LOWER_BOUND_OPERATOR( <= , phoenix::less_equal_eval, phoenix::actor<T>)

        UPPER_BOUND_OPERATOR( < , phoenix::less_eval)
        UPPER_BOUND_OPERATOR( <= , phoenix::less_equal_eval)

    }

}


namespace index {
    using namespace boost::phoenix;
    boost::phoenix::actor<boost::phoenix::argument<0> > const i;
    boost::phoenix::actor<boost::phoenix::argument<1> > const j;
    boost::phoenix::actor<boost::phoenix::argument<2> > const k;
    boost::phoenix::actor<boost::phoenix::argument<3> > const l;

    template<int N>
    range_::detail::index<N> range(const boost::phoenix::actor<
                                   boost::phoenix::argument<N> >&) {
        return range_::detail::index<N>();
    }
    template<int N, class F>
    range_::detail::index<N> range(const boost::phoenix::actor<
                                   boost::phoenix::argument<N> >&,
                                   const F &f) {
        // return range_::detail::index<N>();
        throw std::exception("not implemented");
    }



}

int main(){

    using namespace index;

    // formula domain language rough prototype
    // stuff in brackets can be any valid phoenix lambda expression

    // physicist notation, lower bound may be implicit
    (range(i) <= j, 3 <= range(j) < 4)[std::cout << i << " " << j << std::endl];

    // implicit physicist notation, not done yet
    //(range(i) < range(j) < 4)[...]

    // programmer notation, same as above , but order is reversed
    (3 <= range(j) < 4)(range(i) <= j)[std::cout << i << " " << j << std::endl];

    // ignore, some early prototype for lambda tensor
    // size_t N = 4;
    // tensor::tensor<4> T(N,N,N,N);

     // tensor::function<tensor::tensor<4> > T_(T);
    // (range(j) < 4)(range(i) <= j)[std::cout << T_(i,j,0,0)];

    // (range(i) < j, range(j) < N)[T_(i,j,0,0) = T_(j,i,0,0)];
    // sum(j < val(N))[T_(i,j,0,0)];

}

Answer 9

If you're looking for simplicity you should take the implicitness of the loops even further. E.g., something like this

T( i < j , j < N ) = ( T(i,j) - T(j,i) )/e(i+j)

will work if you rewrite the assignment operator = to behave normally for something like a(i) = b(i) + c(i) but behave like a summation for a(i<5) = b(i) + c(i). Assume summation starts from 0 unless the lower limit is specified, e.g. a(3<i<5), check for symbolic upper/lower limits that appear as summation indices and make double sums as necessary. If you want the syntax to force explicitness you could define a separate sum operator s=

T( i < j , j < N ) s= ( T(i,j) - T(j,i) )/e(i+j)

I don't think you can get any cleaner than this and still have some general purpose usability. As for your short term goal, using the notion of specifying the summation index at the same time that the index first appears you could write.

E_MP2 s= EV( i < n1 , j < n2 , a < n3 , b < n4 ) *
         2 ( EV(a,b,i,j) - EV(a,b,j,i) ) / ( e(i)+e(j)-e(a)-e(b) )

where you explicitly state that this is a sum (using s=) making that operator then take the summation indices and limiting values from the first instance an index appears. Specifically you could also use a syntax like (assuming now a,b fixed and i,j as per your example)

E_MP2 s=(i<j,j<N) EV(i,j,a,b) *
                  2 ( EV(a,b,i,j) - EV(a,b,j,i) ) / ( e(i)+e(j)-e(a)-e(b) )

which is quite clear notationally.

You could then go on and take this concept even further by, e.g., defining an integration operator i= that does the same thing. I.e. it looks for instances of variables that are marked down with limits and then proceeds to integrate the expression with respect to those variables

F i=(0<x<Pi) x^-1 * exp(-I x^2)

similarly to the summation you could specify the limit when x first occurs

F i= x[0,Pi]^-1 * exp(-I x^2)

where the square brackets serve to differentiate the notation from summation, so that you don't have to use i= or s= and can use both summation and integration at the same time:

F(i) = G(i,j<10) * x[0,inf]^-1 * H(i,j,x)

Answer 10

You may want to look at APLish languages for inspiration. By working with the matrix/array as a whole, you can get the brevity down quite a bit. I'm going to use Q below, and unless I misread your post, your second statement can be written as:

sum raze (T-flip T) div e

To understand T minus flip T, you need to look at an example. Imagine we have T set to the following matrix:

0 1 2
3 4 5
6 7 8

flip T swaps the top two dimensions, which results in:

0 3 6
1 4 7
2 5 8

So T-flip T is basically T(i,j)-T(j,i) but a lot less typing, and thus a lot less error-prone.

The raze reduces an array to a single dimension, so razing this:

0 3 6
1 4 7
2 5 8

turns it into this:

0 3 6 1 4 7 2 5 8

Finally, the sum is sum-over; it basically adds up all of the members of its list, so

sum 0 3 6 1 4 7 2 5 8

means:

0+3+6+1+4+7+2+5+8

Implementing this kind of thing in C++ isn't that difficult; you could:

sum(raze((T-flip(T))/e))

with the right level of operator overloading.

By the way, K is even more brief:

+/,/(T-+:T)%e

Answer 11

Encapsulate!

I'm sure you'll find some syntax that balances concision and clarity. However good it is, it will be vastly improved by providing encapsulation. So instead of

qty = sum(range(i) < j < N))[(T(i,j) - T(j,i))/e(i+j)];

You could have

Texpr = (T(i,j) - T(j,i))/e(i+j);
RangeExpr = (range(i) < j < N);
qty = sum(RangeExpr)[ Texpr ];

That might afford you more verbosity in the syntax.

PS: Isn't this Mathematica? Mathematica C/C++ Language Interface

Answer 12

I would give a good read to the Project Fortress blog, it has some inspiring posts on mathematical concise notations for a programming language.

Answer 13

You should have a look at syntax used for Haskell's list comprehension.