Number of iterations in nested for-loops?

Question

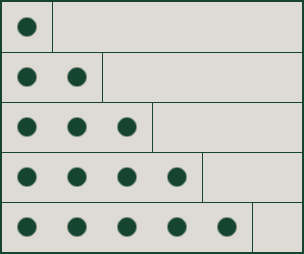
So I was looking at this code from a textbook:

for (int i=0; i<N; i++)
   for(int j=i+1; j<N; j++)

The author stated that the inner for-loop iterates for exactly N*(N-1)/2 times but gives no basis for how he arrived to such an equation. I understand N*(N-1) but why divide by 2? I ran the code myself and sure enough when N is 10, the inner loop iterates 45 times (10*9/2).

I messed around with the code myself and tried the following (assigned only i to j):

for (int i=0; i<N; i++)
   for(int j=i; j<N; j++)

With N = 10, this results in 55. So I'm having trouble understanding the underlying math here. Sure I could just plug in all the values and bruteforce my way through the problem, but I feel there is something essential and very simple I'm missing. How would you come up with an equation for describing the for loop I just constructed? Is there a way to do it without relying on the outputs? Would really appreciate any help thanks!

Answer 1

Look at how many times the inner (j) loop runs for each value of i. When N = 10, the outer (i) loop runs 10 times, and the j loop should run 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 times. Now you just add up those numbers to see how many times the inner loop runs. You can sum the numbers from 0 to N-1 with the formula N(N-1)/2. This is a very slight modification of a well-known formula for adding the numbers from 1 to N.

For a visual aid, you can see why 1 + 2 + 3 + ... + n = n * (n+1) / 2

Answer 2

You're looking at nested loops where the outer one runs N times and the inner one (N-1). You're in effect adding up the sum of 1 + 2 + 3 + ....

The N * (N+1) / 2 is a "classic" formula in mathematics. Young Carl Gauss, later a famous mathematician, was given in-class busywork: Adding up the numbers from 1 to 100. The teacher expected to keep the kids busy for an hour but Carl came up with the answer almost immediately: 5050. He explained: 1 + 100; 2 + 99; 3 + 98; 4 + 97; and so on up to 50 * 51. That's 50 sums of 101 each. You could also see that as (100 / 2) * (100 + 1); that's where the /2 comes from.

As for why it's (N-1) instead of the (N+1) I mentioned... that could have to do with starting from 1 rather than 0, that would drop one iteration from the inner loop, I think.

Answer 3

Think about what happens each time the outer loop iterates. The first time, i == 0, so the inner loop starts at 1 and runs to N-1, which is N-1 iterations in total. The next time through the outer loop, i has incremented to 1, so the inner loop starts at 2 and runs up to N-1, for a total of N-2 iterations. And that pattern continues: the third time through the outer loop, you get N-3 iterations, the fourth time through, N-4, etc. When you get to the last iteration of the outer loop, i == N-1, so the inner loop starts with j = N and stops immediately. So that's zero iterations.

The total number of iterations is the sum of all these numbers:

(N-1) + (N-2) + (N-3) + ... + 1 + 0

To look at it another way, this is just the sum of the positive integers from 1 to N-1. The result of this sum is called the (N-1)th triangular number, and Wikipedia explains how you can find that the formula for the n'th triangular number is n(n+1)/2. But here you have the (N-1)th triangular number, so if you set n=N-1, you get

(N-1)(N-1+1)/2 = N(N-1)/2

Answer 4

If you count the iterations of the inner loop, you get:

1 2 3 4 5 6 7 8 9 10

To get the total for an arbitrary number of iterations, you can "wrap" the numbers around like this:

0 1 2 3 4 
9 8 7 6 5

Now, if we add each of those columns, the all add to 9 (N-1), and there are 5 (N/2) columns. It's pretty obvious that for any even N, we'd still get N/2 columns that each added up to (N-1). As such, when the total number of iterations is even, the total number of iterations is always (N/2)(N-1), which (thanks to the commutative property) we can rewrite as N(N-1)/2.

If we did the same for an odd number of iterations, we'd have one "odd" column that couldn't be paired. In this case, we can ignore the '0' since we know it won't affect the overall sum in any case. For example, let's consider N=9 instead of N=10. For that, we get:

1 2 3 4
8 7 6 5

This gives us (N-1)/2 columns (9-1=8, 8/2=4) that each add up to N, so the sum will be N*(N-1)/2. Even though we've arrived at it slightly differently, this is an exact match for the formula above for when N is even. Again, it seems pretty obvious that this would remain true regardless of the number of columns we used (i.e., total number of iterations).

For any N (odd or even), the sum of the numbers from 0 through N-1 is N*(N-1)/2.