What's a good algorithm to generate a maze?

Question

Say you want a simple maze on an N by M grid, with one path through, and a good number of dead ends, but that looks "right" (i.e. like someone made it by hand without too many little tiny dead ends and all that). Is there a known way to do this?

Answer 1

Strangely enough, by slightly changing the 'canonical' rules and starting from a random configuration, Conway's Game of Life (I don't know why my Wikipedia link is not working!) seems to generate pretty nice mazes!

(I don't remember the exact rule, but it's a very simple modification that tends to 'densify' the population of cells...)

Answer 2

I would ask Dr Falken. He's good with mazes. I'm slightly surprised that he has a MySpace account. Who knew!

Answer 3

From http://www.astrolog.org/labyrnth/algrithm.htm

Recursive backtracker: This is somewhat related to the recursive backtracker solving method described below, and requires stack up to the size of the Maze. When carving, be as greedy as possible, and always carve into an unmade section if one is next to the current cell. Each time you move to a new cell, push the former cell on the stack. If there are no unmade cells next to the current position, pop the stack to the previous position. The Maze is done when you pop everything off the stack. This algorithm results in Mazes with about as high a "river" factor as possible, with fewer but longer dead ends, and usually a very long and twisty solution. It runs quite fast, although Prim's algorithm is a bit faster. Recursive backtracking doesn't work as a wall adder, because doing so tends to result in a solution path that follows the outside edge, where the entire interior of the Maze is attached to the boundary by a single stem.

They produce only 10% dead ends

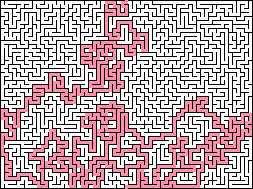
is an example of a maze generated by that method.